Программ для расчета выкроек - Программа построения выкроек для конусов Математика для

Методика построения основы лифа
Гремим пожарными ведрами. Задача о пожарном ведре: схема решения. Решение задачи о пожарном ведре.

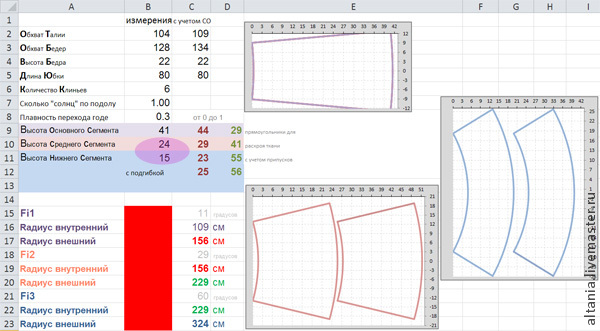






Программа Cones предназначена для построения выкроек разверток конусов с круглым и овальным основанием, полных и усеченных, прямых и наклонных. Выкройка может быть продублирована до такого количества экземпляров, которое помещается на странице размером х мм. Страница с выкройками может быть распечатана или сохранена в виде файла векторной графики в формате EMF для дальнейшего использования ее в графическом редакторе. Формулы, по которым строится выкройка для круглого прямого конуса, описаны в статье Выкройка для конуса. Алгоритмы, по которым строится выкройка для овального и наклонного конуса, описаны в статье Выкройка овального и наклонного конуса. Подробная инструкция для пользователя находится в файле справки ConesHelp.
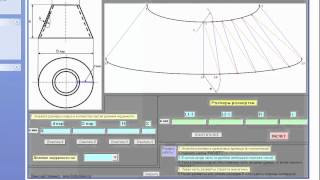
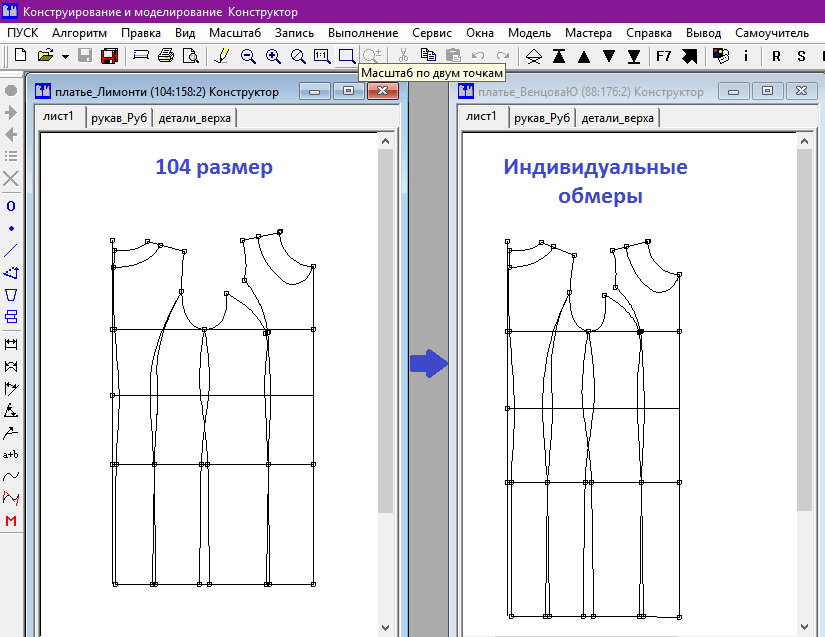

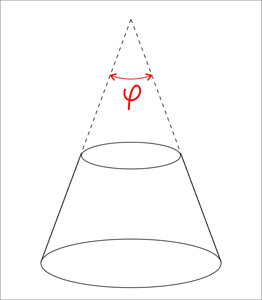


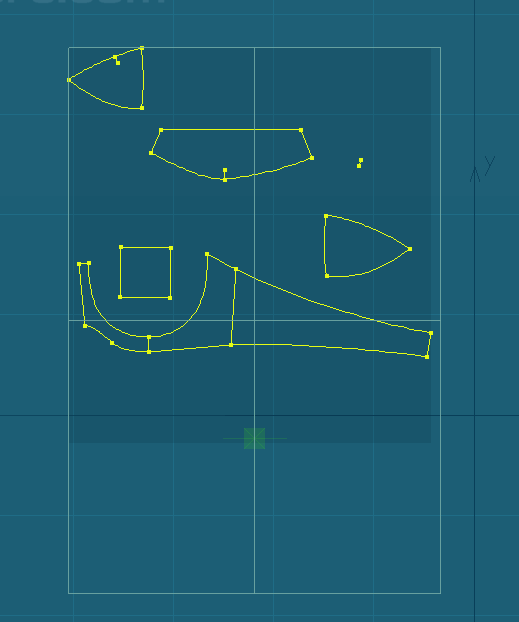




Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости. Картинка ниже иллюстрирует задачу. Про конус нам известен радиус основания и высота конуса или высота усеченного конуса. Для описания развертки нам надо найти радиус внешней дуги, радиус внутренней дуги если конус усеченный , длину образующей и центральный угол. Длину образующей можно посчитать по теореме Пифагора: , при этом для полного конуса r1 просто обращается в ноль.



Похожие статьи
- Вкусно на телеканале подмосковье из программы вкусно - Лаваш в домашних условиях, рецепты с фото на
- Сова своими руками с инструкцией - Выкройки сов. Большая подборка выкроек / Мастер-класс
- Упражнения по шейпингу в домашних условиях - Образовательная программа Росписи по дереву
- В программе фестиваля мастер-класс - Первый Международный фестиваль мастер-классов Слава